Formation SCILAB (fonctions avanc�es)

SCILAB est un logiciel libre de calcul scientifique, d�velopp� � l'origine en France par l'INRIA (Institut National de Recherche en Informatique Appliqu�e) et maintenu maintenant par Scilab Entreprise. SCILAB permet de travailler � tr�s haut niveau (les objets de base sont les matrices), et est fournit avec de tr�s riches biblioth�ques de traitement num�rique (alg�bre lin�aire, traitement du signal, contr�le, etc.).

Cet atelier de formation fournira aux participants un ensemble de savoir-faire avanc�s autour de l'outil SCILAB leur permettant de traiter des probl�mes relatifs � l'analyse de donn�es num�riques, � la mod�lisation de syst�mes et au prototypage de solutions � base de traitements num�riques.

Dur�e de la formation

Trois jours

Date et lieu de la formation

Lieu : Toulouse, date : sur demande.

Inscription

Formulaire d'inscription disponible ici.

Contenu

I - INTRODUCTION A SCILAB
Durant cette premi�re partie, nous allons faire un tour d'horizon de l'environnement SCILAB, et des principales fonctions (calcul scalaire et matriciel, fonctions graphiques, programmation).
Introduction : Domaines d'application, description du contexte (par rapport aux autres applications de calcul) Environnement : console SCILAB, aide en ligne, �diteur, El�ments de base du langage : Nombres r�els et complexes, matrices et vecteurs, constantes, booleans, polyn�mes et fractions rationnelles, fonctions math�matiques usuelles. Programmation :scripts et fonctions, structures de contr�le, mise au point, entr�es / sorties fichiers Visualisation des donn�es : repr�sentations 2D et 3D, axes et l�gendes.
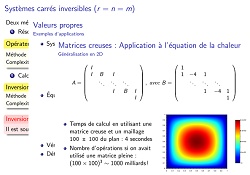
II - ALGEBRE LINEAIRE
SCILAB est fourni avec des fonctions tr�s avanc�es pour l'alg�bre lin�aire, permettant de traiter aussi bien des syst�mes dits denses (� faible dimension), que des syst�mes creux. De plus, le langage de SCILAB �tant fond� sur les matrices, vous verrez que le calcul matriciel s'en trouve tr�s simplifi� !
Syst�mes lin�aires : syst�mes inversibles, surd�termin�s, sous d�termin�s, conditionnement, R�solution au sens des moindres carr�s, pseudo inverse Valeurs propres et vecteurs propres. D�compositions matricielles et applications (LU, QR, SVD, . . .) Probl�mes � grande dimension
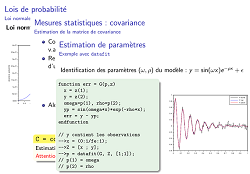
III - STATISTIQUES
M�me si ce n'est pas sa sp�cialit�, SCILAB inclus les fonctions les plus importantes pour simuler des processus al�atoire ou estimer des param�tres.
Lois de probabilit�s / fonctions de r�partion Simulation : g�n�rateurs congruents (limites), lois usuelles, permutations Statistiques simples : moyenne, variance, m�diane, quantiles, . . . Estimation de param�tres : Estimation au maximum de vraisemblance / moindre carr�s. Cas particulier : r�gression lin�aire
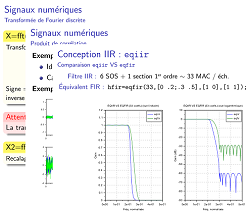
IV - TRAITEMENT DU SIGNAL
Nous allons voir comment SCILAB peut vous aider pour l'analyse des donn�es exp�rimentales (analyse fr�quentielle, corr�lations, etc.) et la conception et l'analyse de filtres num�riques (FIR, IIR).
Signaux num�riques : �chantillonnage, transform�e de Fourier Repr�sentation des syst�mes lin�aires discrets : �quation aux diff�rences, fonction de transfert, repr�sentation d'�tat (state/space). Analyse (temporelle, fr�quentielle, p�les / z�ros) Conception des filtres num�riques : FIR (fen�tr�e, Remez), IIR (� partir de prototypes analogiques, factorisation en sections du second ordre), quantification Interpolation : Interpolations lin�aire, splines, interpolations 2D Estimation spectrale : M�thodes non param�triques (p�riodogrammes) / param�trique (ARMA)
V - CALCUL DIFFERENTIEL / SIMULATION / OPTIMISATION
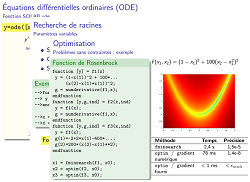
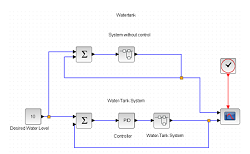
La simulation des syst�mes physiques n�cessite souvent la r�solution num�rique d'�quations diff�rentielles : nous allons faire un tour d'horizon des fonctions correspondantes dans SCILAB. Ensuite, nous allons voir les fonctions principales de la biblioth�que d'optimisation num�rique, qui permet de trouver des solutions optimales � divers probl�mes pratiques (trajectoires optimales, affectation de ressources, etc.).
Equations diff�rentielles : ODE (premier ordre et ordre sup�rieur), forme implicite, cas particuliers des SLC et SLD, probl�mes hybrides, DAE. Probl�mes aux valeurs limites. Int�gration num�rique Probl�mes � contraintes fixes : Fonctions non diff�rentiables, diff�rentiables. Cas particuliers : moindres carr�s non lin�aires et lin�aires. Probl�mes � contraintes lin�aires : Programmation lin�aire et quadratique R�solution des �quations non lin�aires
VI - AUTRES FONCTIONS (APERCU)
Pr�sentation rapide de l'outil graphique XCos pour la simulation des syst�mes, Pr�sentation rapide de quelques bo�tes � outils additionnelles : ondelettes, traitement d'image

Travaux pratiques

Tout au long de l'atelier l'ensemble des points abord�s sera illustr� par des exemples et de petits exercices qui vous permettront de mettre en oeuvre directement les notions vues dans SCILAB.